Notes on Atomic Structure For BSc, GE and Entrance Examinations

Notes on Atomic Structure

Bohr's Atomic Model

    In 1913, Niels Bohr brought an atomic model that could manage an excellent balance between classical and quantum mechanical interpretation. A model that could compensate and explain the shortcomings and imperfections in the previous atomic models.

    The important postulates of the Bohr's atomic model are:

1. The electrons in an atom revolve round the nucleus only in certain permitted circular path called the shells or energy levels or stationary states.

2. Each energy level is  denoted with a principal quantum number 'n'. Where n = 1, 2, 3, .....

3. The shell or energy level closest to the nucleus is denoted with n = 1 or the K shell, the next one with n = 2 or L shell and so on .....

4. These energy levels are associated with definite amount of energies, given by the formula:

    E_n = -KZ² / n² where K = 13.6 ev, Z = atomic number and n = number of orbit from the nucleus.

5. The distance r of a shell from the nucleus is given by the formula,

r_n = a₀ n² / Z , where a₀ = Bohr’s first orbit radius = 0.529 A⁰

6. So long as the electron revolves in a particular orbit, it neither absorbs nor emit energy. This is the reason why it does not fall into the nucleus. In this way Bohr compensated the shortcoming of the Rutherford's Atomic Model

7. An electron gets excited to the higher energy levels when ever it absorbs energy. This energy is equal to the difference between the energies of two concerned energy levels.

ΔE = E_f - E_i , where E_f = energy of final orbit and E_i = energy of initial orbit

Also when an electron jumps from a higher orbit to the lower orbit, then difference in energy (E_f - E_i) is emitted.

This is the key explanation of the hydrogen spectrum.

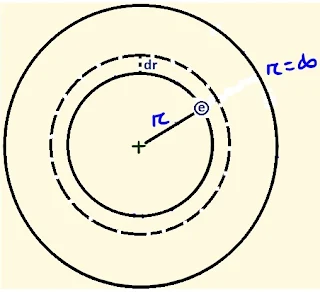
8. Only those orbit are allowed for the electrons to revolve round the nucleus, for which the angular momentum (mvr) of the electron is a whole number multiple of h/2π. Mathematically, mvr = nh/2π. This principle is called quantisation of angular momentum.

9. The above postulates can be developed to reach at the conclusion that the circumference of an orbit (in which an electron revolves) is equal to the whole number multiple of the wavelength of the electron. mathematically, 2πr = nλ

10. The most important of all the postulates is the force balance equation. The centrifugal force of a revolving electron acting outward is counterbalanced by the electrostatic force (centripetal force) between electron and nucleus acting inward. 

i.e., mv² /r = (1/4πε₀) (Ze²/r² )

This is the reason why electron does not fall into the nucleus and moves in a definite circular path.

Calculation of radius of nth orbit:

Applying force balance (i.e., centrigugal force = centripeatal force) equation:

mv² /r = (1/4πε₀) (Ze²/r² )

=> v² = Ze²/4πε₀ mr .......... eq. 1

since mvr = nh /2π

=> v = nh /2πmr

=> v² = n²h² /4π²m²r² …… eq.2

From eq 1 and 2,

n²h² /4π²m²r² = Ze²/4πε₀ mr

=> r = n²h² ε₀ / πme²z

=> r = (h² ε₀ / πme²) (n²/Z)

=> r = a₀ (n²/Z) where a₀ = (h² ε₀ / πme²) = Bohr’s first orbit radius for hydrogen atom

Putting the value of constants, we get a₀ = 0.529 A⁰ = 0.0529 nm

For hydrogen atom, Z = 1

If n =1, r₁ = a₀ = 0.529 A⁰

If n =2, r₂ = 4a₀ = 4 X 0.529 A⁰

^{CLICK ME -GET ALL CHEMISTRY NOTES}

Problem 1: Determine the second Bohr's orbit of He⁺ ion.

Solution: The atomic number of He⁺ ion = z = 2

Second Bohr's orbit => n = 2
=>r₂ = a₀ n² / Z = 0.529 (2² / 4) = 2 X 0.529 A⁰

Problem 2: Establish a relationship between the nth Bohr's orbit of Hydrogen and He⁺ ion.
Solution: r = a₀ (n²/Z)
r(H) = a₀ (n²/Z) = a₀ n²
r (He⁺) = a₀ (n²/Z) = a₀ (n²/2)
r(H)/r(He⁺) = 2 
=> r(H) = 2 r(He⁺)

Get Notes on Gaseous State for BSc

Velocity of an electron in nth Bohr’s Orbit:
We know mvr = nh / 2π
=> v = nh/2πmr
Putting the value of  r = a₀ n² / Z
V = (h/2 πm a₀) (z/n)
Putting the values of the constants we have,
Vn = velocity of Bohr's nth orbit = 2.18X10⁶ (z/n)m s^-1

Problem: Determine the speed of an electron moving in the second orbit of unipositive helium ion.
Solution: We have Vn = 2.18X10⁶ (z/n)m s^-1
For He⁺ ion, z = 2, Second Bohr's orbit => n = 2
=> Vn = 2.18X10⁶ m s^-1

Note: The formula of velocity of electron in nth Bohr's orbit indicates that, all hydrogen like species having same z and n will have velocity equal to 2.18X10⁶ m s^-1

Assignment: Determine the Bohr's orbit of Li2+ ion in which the electron moves at a speed equal to the speed of electron in the first Bohr's orbit of  hydrogen.

Revolution per second (RPS) in nth Bohr's Orbit around nucleus:
The number of revolutions per second (RPS) ∝ Velocity of electron (V)
The number of revolutions per second (RPS) ∝ 1/circumference of orbit (2πr)
=> The number of revolutions per second (RPS) = V/2πr
Putting the value of V = nh/2πmr 
RPS = (nh / 4π²mr²)
and r = a₀ n² / Z
=> RPS = (nh/4 π²m) (z²/ a₀ n²)²
=> RPS = (h/4π²m a₀²) (z² /n³)
Putting the values of the constants,
=> RPS = 6.584X10¹⁵ (z² /n³) revolutions /s

Assignment: Calculate the number of revolutions per second made by an electron in the second Bohr's orbit of He+ ion.

Get Notes on Periodic Classification of Elements

Energy of an electron in nth Bohr's Orbit: 

The sum of the kinetic and potential energy of the electron moving in an orbit gives its total energy. E(Total) = K.E + P.E

K.E  = ½ (mv²)

Since mv² /r = Ze²/4πε₀ r²

½ (mv²) = Ze²/8πε₀ r = K.E

    Potential energy of the electron is the energy possessed by it due to its position w.r.t. the nucleus. Consider an electron present at infinite distance apart from the nucleus, where its energy is considered to be zero. As it comes closer to the nucleus (into the influence of nucleus) it looses energy, hence its energy becomes negative when it is placed in any orbit.

    Its now clear from the above logic that the potential energy of an electron in a given Bohr's orbit is the negative of the work done required to move that electron from the said Bohr's orbit to the infinity Bohr's orbit.

Since work done = Force X Displacement
An infinitesimal work done by an infinitesimal displacement of the electron is given by, dW = F dr

Thus the total work done in displacing the electron to the infinity orbit should be,

Hence total energy (E) = K.E + P.E
=  (Ze²/8πε₀ r) + (- Ze²/4πε₀ r) = - Ze²/8πε₀ r
Putting the value of r = a₀ n² / Z
E (Total) = - Z²e²/8πε₀ n² = (- e²/8πε₀)( Z²/n²)
E (Total) = - Z²e²/8πε₀ n² = (- e²/8πε₀) (Z²/n²)
Putting the values of constants we get,
En =Energy of nth Bohr's orbit = - K (Z²/n²)
Where K = 13.6 ev = 2.18 X 10^-18 J

Problem: Calculate the energy of electron in the Bohr's first orbit of hydrogen atom in kilo Joule per mole.

Solution: For hydrogen atom, Z = 1 and n =1
E₁=  - K (Z²/n²) = - 2.18 X 10^-18 Joule / atom = - 2.18 X 10^-18 J X 6.02 X 10²³ Joule/ mole
= - 2.18 X 10^-18 J X 6.02 X 10²³ x 10^-3 K Joule / mole = - 1312 K Joule / mole

Transition Energy and Ionisation Energy: When ever an electron jumps from any initial orbit (n_i) to the final one (n_f), energy is absorbed or lost depending on whether it jumps up or down respectively.

Mathematically, the energy absorbed or lost = ΔE = E_f - E_i 
=> ΔE = - K (Z²/n_f²) - {- K (Z²/n_i²)} = KZ² {(1/n_i²) - (1/n_f ²)} 

When an electron absorbs energy and jumps to such an orbit (or such a distance from the nucleus) so that the nucleus will have no more influence on the concerned electron, then the amount of energy absorbed by the electron is called the ionisation energy. The final orbit in this case, n_f = ∞
    Thus ionisation energy, 

ΔE = KZ² {(1/n_i²) - (1/n_f²)}

= KZ² {(1/n_i²) - (1/∞²)}

= KZ²/n_i²

Problem: Calculate the energy required to excite an electron of hydrogen atom from first Bohr's orbit to the third orbit and also calculate the amount of energy emitted when the same electron jumps down from that 3rd Bohr's orbit to the first one.

Solution:  ΔE = KZ² {(1/n_i²) - (1/n_f²)}

    For hydrogen atom, Z = 1, when electron jumps up from first to the third orbit, 

n_i = 1 and n_f = 3. Thus ΔE = K {(1/1²) - (1/3²)}

= 8/9 K

= 8/9 X 13.6 eV amount of energy is gained.

   When the electron jumps down from third Bohr's orbit to the first one in hydrogen atom, n_i = 3 and n_f = 1.

Thus ΔE = K {(1/3²) - (1/1²)}

= - 8/9 K

= -8/9 X 13.6 eV

That means the same amount of energy is released.

Problem: Determine the third ionisation energy of lithium atom.

Solution:  After the loss of two electron lithium becomes a hydrogen like species (having only one electron). The amount of energy required to eject the third electron out of the influence of lithium nucleus is called its third ionisation energy.

 Z = 3, n_i = 1,    ΔE = KZ²/n_i²

    Thus ionisation energy = 9K = 9 X 13.6 eV = 122.4 eV

Emission Spectrum of Hydrogen atom: 

Electrons of hydrogen atoms when absorb energy, get excited to the next higher shells. These excited electrons emit energy (in form of light), when they jump down to the lower energy levels. These energy (emitted light) are observed on a fluorescent screen which appear as group of lines. The number of lines observed on the screen indicates the number of possible transitions made by excited electrons.

    If the energy levels are shown as their increasing energy and quantum numbers, we get the following.

    The actual line spectra of hydrogen looks like the following:

    Hydrogen being the simplest atom (containing one electron and one proton) has the simplest emission spectrum. The energy of transition for any line is expressed in terms of wave number as follows:

ΔE = KZ² {(1/n_i²) - (1/n_f²)}

=> ΔE = hν = hc/λ = KZ² {(1/n_i²) - (1/n_f²)}

=> 1/λ = ṽ = (KZ²/hc) {(1/n_i²) - (1/n_f²)} 

=> ṽ =  R_H Z² {(1/n_i²) - (1/n_f²)} ,  

Where R_H = K/hc = Rydberg's constant = 1.0973 X 10⁷ m^-1

1/λ = ṽ = wave number

    As is shown in the above figure,  the group of closely spaced lines (called a series) represent the transition of electrons from any higher energy levels to a fixed lower energy level.  

The series of lines placed to the extreme left (see the figure above) around 100 nm is called the Lyman Series. This series corresponds to the shortest wavelength which fall in the ultraviolet region. 

For this series, n_i = 1 and n_f = 2, 3, 4, .... The first line of the series is represented as Ly-α for which n_i = 1 and n_f = 2.

    In Balmer series, n_i = 2 and n_f = 3, 4, 5, .... This series falls in the visible and near infrared region. 

    In Paschen series, n_i = 3 and n_f = 4, 5, 6, .... This series falls in the infrared region of the electromagnetic spectrum. 

    In Brackett series, n_i = 4 and n_f = 5, 6, 7, .... This series falls in the infrared region.

   In Pfund series, n_i = 5 and n_f = 6, 7, 8,  .... This series falls also in the infrared region.

    Note: The maximum number of lines that can be obtained when an electron jumps down from nth orbit to the ground state = n (n-1)/2. For example if an electron jumps down from 6th orbit (n=6) the number of spectral lines = 6(6-1)/2 = 15

Problem: What will be the frequency and wave number of the second line of Balmer series.

Solution: For Balmer Series, n_i = 2 and its second line has n_f = 4

=> 1/λ = ṽ = wave number 

= R_H Z² {(1/n_i²) - (1/n_f²)} , 

Since C = νλ =>  ν = frequency

= C/λ = C . ṽ

= C . R_H Z² {(1/n_i²) - (1/n_f²)} 

put value for n_i and n_f

C = 3 X 10⁸ m/sec

RH = 1.0973 X 10⁷ m^-1

and then get answer.

Correctness or Validity or Advantages of  Bohr's Atomic Model:

1. It explains the spectrum almost clearly including emission and absorption spectrum along with hydrogen spectrum. Electrons in atoms absorb energy and get excited to the higher energy levels and when they return back to the lower energy levels they emit energy.

2. As long as electrons move in a definite orbit they do not gain or loose electrons. This makes an atom stable. Thus Bohr explained the stability of atoms.

3. The theoretical values of the spectral lines as predicted by Bohr is almost equivalent to the experimental values obtained by eminent scientists Rydberg and Ritz.

4. Ionisation energy can be calculated with accuracy from Bohr's transition energy formula.

5. Since there is no force available to counter balance the force of attraction of the nucleus on the electron, a centrifugal force must be there due to the circular motion of the electron. This proves that the electrons are not stationary but they move.

Disadvantages or Drawbacks or Limitations of Bohr's Atomic model:

1. It fails to explain the spectra of multi electron species.

2. By Bohr's prediction the the path of the electrons are circular whereas modern study indicates 3 dimensional motion of the electrons. In addition to this the stationary state concept has been discarded by Heisenberg's uncertainty principle.

3. It is unable to explain the fine lines present inside a spectral lines when seen under powerful microscope and also fails to explain the splitting of spectral lines under external magnetic field (the finer spectral lines as shown by Zeeman).

Sommerfeld's Atomic Model

Sommerfeld’s atomic model is an improvement over Bohr’s atomic model. It was Introduced by Arnold Sommerfeld in 1916, which refined Bohr's theory by incorporating the concept of elliptical orbits and relativistic corrections. While Bohr focused on the circular path called orbit or Shell, Sommerfeld introduced a new type of elliptical path for electrons to explain the splitting of fine lines obtained in Hydrogen spectrum. His theory helped to understand how subshells make a shell.

Postulates of Sommerfeld’s Atomic Model

Sommerfeld refined Bohr’s atomic model by introducing elliptical orbits and relativistic corrections. His postulates are:

1. Electrons Move in Discrete Orbits

Similar to Bohr’s model, Sommerfeld stated that electrons revolve around the nucleus in definite orbits without radiating energy.

2.Azimuthal Quantum Number and Sub-Shells

Sommerfeld used the letter k for Azimuthal quantum number but later the letter l was used. He suggested that, for any principal quantum number n, the values of azimuthal quantum number k vary from 1 to n. Each value of the k for any particular value of n represents a different subshell (an eliptical path) under the partuclar shell.

For example, if n=3, then different values of k will be equal to 1 to 3. i.e., 1 and 2 and 3. Thus threee different values of k represent diffrent subshells (eliptical paths) for the electrons. Different possibilities are n=3, k=3 and n=3, k=2 and n=3,k=1

This explained the splitting of energy levels into sub-levels (s, p, d and so on).

3.Introduction of Elliptical Orbits

Unlike Bohr, who proposed circular orbits, Sommerfeld suggested that electrons move in elliptical orbits with the nucleus at one of the foci. 

Circular orbits are a special case of elliptical orbits when the eccentricity is zero. We can futher draw a figure to summerise the postulates 2 and 3.

By CielProfond - Own work, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=150816454

4. Major and Minor Axis of an elliptical path:

The ratio of the length of major axis to the minor axis of any elliptical path is equal to n/k

5. Angular momentum of an electron:

The angular momentum of an electron is equal to kh/2π where k is equal to the azimuthal quantum number.

6.Relativistic Mass Correction

Since electrons moving in inner orbits have high velocity, Sommerfeld applied Einstein’s theory of relativity to correct Bohr’s model.

The faster an electron moves, the greater its mass, leading to slight energy level variations and explaining the fine structure of spectral lines.

7. Fine Structure of Spectral Lines

Sommerfeld’s model successfully explained the fine structure (small splitting) in the hydrogen spectrum, which Bohr’s model failed to do.

8.Zeeman Effect and Stark Effect (Partial Explanation)

Sommerfeld’s model attempted to explain the Zeeman effect (splitting of spectral lines in a magnetic field) and Stark effect (splitting in an electric field), though it was not completely successful.

Drawbacks of Sommerfeld's Atomic Model

1.Failure to Explain Spectral Lines of Multi-Electron Atoms

While Sommerfeld’s model improved upon Bohr’s by explaining fine structure in hydrogen, it could not accurately explain the spectra of atoms with more than one electron.

2.Violation of Uncertainty Principle

The concept of well-defined elliptical orbits contradicts Heisenberg's Uncertainty Principle, which states that the exact position and momentum of an electron cannot be simultaneously determined.

3.No Justification for Elliptical Orbits

The assumption of elliptical orbits was introduced to fit experimental data rather than derived from first principles, making the model less theoretically sound.

4.Inconsistency with Electron Spin

Sommerfeld’s model did not account for electron spin, which was later introduced by Goudsmit and Uhlenbeck to explain additional spectral features.

Conclusion

Sommerfeld’s atomic model was an important step toward modern quantum mechanics. It introduced elliptical orbits, quantum numbers, and relativistic effects, paving the way for Schrödinger’s wave mechanical model of the atom.

Electromagnetic Wave

An electromagnetic (EM) wave is a type of wave that consists of oscillating electric and magnetic fields, which propagate through space at the speed of light. These waves do not require a medium and can travel through a vacuum.

Key Characteristics of Electromagnetic Waves:

Perpendicular Fields:

The electric field (E) and the magnetic field (B) oscillate perpendicular to each other.

Both fields are also perpendicular to the direction of wave propagation, making it a transverse wave.

Speed of Light:

In a vacuum, all EM waves travel at the speed of light (ccc) which is approximately 3.0×10⁸m/s.

Self-Propagating:

A changing electric field generates a magnetic field, and a changing magnetic field generates an electric field. This continuous interaction allows EM waves to propagate.

Energy Transmission:

EM waves carry energy and momentum and can exert pressure, known as radiation pressure.

Electromagnetic Spectrum:

EM waves exist in a broad range of wavelengths and frequencies, forming the electromagnetic spectrum, which includes:

Radio waves (used in communication)

Microwaves (used in cooking and radar)

Infrared waves (felt as heat)

Visible light (what we see)

Ultraviolet (UV) rays (causes sunburn)

X-rays (used in medical imaging)

Gamma rays (emitted by radioactive materials and used in cancer treatment)

Mathematical Representation:

The relation between frequency, speed and wavelength of an EM wave is:

C = f . λ

An electromagnetic wave traveling in the x-direction can be described by:

E=E₀sin⁡(kx−ωt)

B=B₀sin⁡(kx−ωt)

where:

E₀, B₀= maximum electric and magnetic field amplitudes

k = wave number (k=2π/λ ​)

ω = angular frequency (ω=2πf)

f = frequency

λ = wavelength

Problem: Calculate the wavelength of red light having frequency 4.27 X 10¹⁴ Hz.

Solution: C = f . λ 

=> λ = C/f

=> λ = (3 X 10⁸ m/sec) / (4.27 X 10¹⁴)

= 8.9 X10^-7 m = 890 10^-9 m

= 890 nm

Planck's Quantum Theory:

Statement: Energy emitted or absorbed by a body is not continuous but discontinuous in form of discrete energy packets. Each discrete energy packet is called a quantum (or called photon in case of light energy). Energy of a quantum is directly proportional to its frequency and the total energy absorbed or emitted by a body per second is equal to the product of energy of a quantum and the number of quanta absorbed or emitted by a body per second.

Mathematically,

Energy of a quantum, E ∝ f

=> E = h.f, 

where h = Planck’s constant

h= 6.625 X 10³⁴ joule sec.

and f = frequency of each quantum

And the total energy absorbed or emitted by a body per second, E = n.h.f, 

where n = number of quanta absorbed or emitted per second.

Problem: A discharge lamp rated with power of 25 Watt emits yellow light of wavelength 580 nm. How many photons of yellow light does the lamp generate in one second?

Solution: 

Energy = Power X time

= 25 x 1 = 25 joule

Since, E = n.h.f

n = no. of photons = E/(h.f)

=>n = E/[h(C/ λ)]        (Since C =f λ)

=>n = (25 j X 5.8 X 10^-7)/ (6.625 X 10³⁴ X 3 X 10⁸)

= 7.3 X 10¹⁹ photons

de Broglie Concept of Dual Nature of Matter:

Statement: All forms of matter including electrons, protons or neutrons show dual nature. i.e., wave nature and particle nature.

Derivation:

From Planck’s quantum theory,

E = h.f = hc/λ -------1

From Einstein’s equation,

E = mC² --------- 2

From equation 1 and 2,

mC² = hc/λ

=> λ = h/mc = h/p ------- 3

Where p = momentum of the particle.

or p = mass X velocity

Equation 3 is called de Broglie equation

de broglie wavelength of an electron accelerated by a potential difference of v - volts:

If an electron at rest is accelerated by a potential difference of V volts, its kinetic energy,

(1/2) mv² = e.V       (since electrical work done = charge X voltage)

(Note that v stands for velocity whereas V stands for potential)

=> v = {(2eV)/m}^1/2

Substituting for velocity in equation 3,

=> λ = h/m {(2ev)/m}^1/2

=> λ = h/(2meV)^1/2  --------- 4

In the above equation when we put the value of 'h'(Planck's constant), mass and charge of electron and vary the value of Voltage 'V' between 10 to 10,000 volts, we get λ varying between 1.226 A⁰ to 3.977 A⁰ which coincides with the order of X-rays. This has been confirmed experimentally by Davision and Germer.  The diffraction pattern obtained from the electron beam (produced from a tungsten filament) was similar to that of X-ray diffraction. Thus electrons exhibit wave character.

When electrons strike on ZnS screen they create spot of light which do not spread to the surrounding, area confirming its particle character.

Validity of Bohr's Theory Confirmed by de-Broglie equation:

According to Bohr, mvr = nh/2 π

=>2.π.r = nh/mv= nλ (Since λ = h/mv)

The above equation shows that integral number ‘n’ of wavelength ‘λ’ can be accommodated in Bohr’s orbit having circumference 2πr. In other words, there will be always a whole number of waves in an orbit. We can say the electron waves are in phase.

But when 2πr is not equal to whole number multiple of λ, we say the electron waves are out of phase.

Thus de-Broglie justified Bohr’s angular momentum equation.

Significance of de-Broglie equation:

1. The wave character or the wavelength of large objects in motion has no practical significance due to heavier mass and too sall wavelength.

2. The wave character or wavelength of microscopic particle in motion has practical significace due to longer wavelength.

Problem: Calculate de-Broglie wavelength of helium atom moving with velocity 2.4X10² m/s at 27⁰c.

Solution: Mass of 6.02X10²³ (1 mole) helium atoms = 4g

Mass of 1 helim atom = 4/6.02X10²³ g

=6.64X10^-27kg

λ = h/mv

Putting all the values we can get the answer.

Problem: An electron diffraction experiment was performed using electron beam accelerated by a potential difference of 10kV. Calculate the wavelength of the electron beam.

Solution: λ = h/(2meV)^1/2 

Put the value of h, mass and charge of electron and V = 10 X 10³ = 10⁴ volts, and get the answer.

 Heisenberg’s Uncertainty Principle:

Heisenberg's Uncertainty Principle is one of the fundamental ideas in quantum mechanics, proposed by Werner Heisenberg in 1927. It expresses a fundamental limit to the accuracy with which certain pairs of physical properties (called complementary variables) of a particle can be known simultaneously.

Statement using position and momentum as complementary variables:

It is impossible to measure simultaneously both the position (x) and momentum (p) of a microscopic particle with absolute accuracy and certainty.

Mathematically,

Δx⋅Δp ≥ h/4π

Or

Δx⋅mΔv ≥ h/4π

Where = Uncertainty in position and Δp = Uncertainty in momentum (momentum = mass × velocity), Δv = Uncertainty in velocity

h = Planck’s constant ≈ 6.626×10⁻³⁴ Js

This inequality means that the more precisely we know a particle’s position, the less precisely we can know its momentum, and vice versa.

For example:

If a particle is localized very tightly (i.e., we know where it is), its wavefunction is sharply peaked. This means its momentum spectrum is spread out—so its momentum is uncertain.

If a particle has a well-defined momentum (narrow momentum distribution), its position is spread out means it’s not localized.

Other Uncertainty Pairs

The principle isn’t just limited to position and momentum. It applies to other pairs of complementary or conjugate variables, such as:

Energy (E) and Time (t)

Angular momentum (Lz) and Angular position (φ)

For energy and time the mathematical expression will be,

ΔE⋅Δt ≥ h/4π

If the time for which a system remains in a particular energy state is long then its energy will not be well defined. On the other hand, if the time for which the system remains in a particular energy state is short then its energy will bfe more defined.

Limits of Measurement: It’s impossible to design an experiment that simultaneously measures the position and momentum with arbitrary precision.

Example: Electron in an Atom

In an atom, electrons are bound to the nucleus. If you try to localize an electron too closely (small Δx), you need light radiation of shorter wavelength (high energy). When such a radiation strikes an electron, some of the energy is transferred to the electron and the velocity or momentum of the electron changes.  Similarly if light of longer wavelength is used then electron can’t be located with accuracy whereas there will be no change in velocity or momentum.

Significance of uncertainty principle:

1. If we can't determine the exact position of an electron with accuracy then how can we think of a definite path of an electron. For this reason the idea of definite path for an electron has been discarded by the uncertainty priciple.

2. uncwertainty principle is npot applicable to to macroscopic bodies as photons can't alter their position or momentum.

3. By taking proper substitution in the formula, we can show that electron can't exist inside nucleus.

Problem: Calculate the uncertainty in position of a tiny particle with mass equal to 1mg if its uncertainty in its velocity is 5.5X10^-20 m/s.

Solution: 

m =1mg = 10^-3 kg, Δv = 5.5X10^-20 m/s, π = 3.14, Δx = ?

Δx⋅mΔv ≥ h/4π

Put the values and get the answer.

Problem 2: On the basis of Heisenberg's uncertainty principle, show that an electron can not exist inside nucleus. (Radius of nucleus is of the order 10^-15m, mass of electron is = 9.1 X 10^-31 kg, h = 6.626×10⁻³⁴ Js)

Solution: Δx⋅mΔv ≥ h/4π

=> Δv = h/4π.m.Δx

putting all the values we get,

Δv = 5.77x10¹⁰ m/s which is greater than velocity of light which is impossible. Hence electron can’t exist inside nucleus.

Note: 1. If the uncertainty in position is given within ± 1nm, then Δx should be taken (in the range) as 2 nm.

2. If the uncertainty in position given is of the order ± 1nm, then Δx should be taken as 1nm.

3. If the uncertainty in velocity is given within ± 1m/s, then Δv should be taken (in the range) as 2 m/s.

4. But if the uncertainty in velocity is given as 500 ± 1m/s, then Δv should be taken as ± 1m/s.

Schrodinger’s Wave Equation:

Schrodinger developed a mathematical differential equation whose solution could give the electron distribution around nucleus as well as the allowed energy levels of a particle (electron) in a given field.

Let us consider an electron wave moving along x- axis and behaving like a standing wave. The amplitude function for this wave can be written as:

Watch this Lecture Video for the derivation of Schrodinger Wave Equation

Quantum Numbers:

    The idea of shell was made from Bohr’s atomic model and the idea of Subshells under a Shell was made from the Sommerfeld’s atomic model.

    When spectra producing atoms were placed in a magnetic or electric field and studied using high resolving equipment, several single lines were found to split into component lines. This phenomena lead to the idea of Orbitals under a Subshell.

    Quantum numbers describe the state and behavior of electrons in an atom. Since electrons are governed by the principles of quantum mechanics, we can’t pinpoint their exact location—only probabilities. These four quantum numbers help define the "address" or unique identity of each electron in an atom.

    The first three quantum numbers (Principal, Azimuthal and Magnetic Quantum Numbers) were obtained while solving Schrodinger's wave equation for hydrogen and other atoms.

1. Principal Quantum Number (n)

What It Tells Us:

>  The energy level (or shell) the electron occupies.

> The distance from the nucleus—higher n means farther from the nucleus and higher energy.

> Defines the size of the orbital.

Values:

n = 1, 2, 3, 4... (Positive integers) which represent K, L, M, N, .... Shells respectively.

Effects:

As n increases:

> Energy increases

> Orbital size increases

> Electron is less tightly bound to the nucleus.

> Number of electrons in corresponding shell increases by the formula 2n². That means when n = 3 (M Shell), the number of electron in it = 2X3² = 18.

2. Azimuthal Quantum Number (ℓ)

What It Tells Us:

> The shape of the orbital

> Defines the subshell within a given principal shell

Values:

> For any value n, ℓ = 0 to (n – 1)

For example, if we wish to find the subshells under a shell for which n = 3, then the ℓ values under it are 0 to 3-1.

i.e., ℓ = 0,

ℓ = 1,

and ℓ = 2

> The value of ℓ, its designation and shape is given in the following table.

ℓ	Subshell	Shape
0	s	Spherical
1	p	Dumbbell
2	d	Cloverleaf
3	f	Complex

> Any shell with principal quantum number n has n number of subshells. For example the M shell (n = 3) has three subshells. They are 3s, 3p and 3d subshells.

> Determines the angular momentum of the electron in any subshell by the formula, mvr = (h/2π) [ℓ(ℓ+1)]^1/2

> The maximum number of electrons in a subshell is given by the formula 2(2ℓ+1).

> Thus maximum electrons that can be accommodated in an s – subshell (ℓ=0) = 2(2X0+1) = 2

> Thus maximum electrons that can be accommodated in an p – subshell (ℓ=1) =6

> Thus maximum electrons that can be accommodated in an d – subshell (ℓ=2) = 10

> Thus maximum electrons that can be accommodated in an f – subshell (ℓ=3) = 14

3. Magnetic Quantum Number (mₗ)

What It Tells Us:

> The orientation (preferred region in space) of the orbital in 3D space

> Distinguishes between different orbitals within the same subshell

 Values:

> For any given subshell with Azimuthal quantum number value ℓ, magnetic quantum numbers under this subshell are given by the formula, mₗ = –ℓ to +ℓ (including 0).

> The number of orbitals in a given shell with value ℓ is given by the formula 2ℓ+1.

 > The value of ℓ, possible mₗ values and the number of orbitals under a given subshell is given in the following table.

ℓ	mₗ values	Orbitals Count
0	0	1 (s)
1	–1, 0, +1	3 (p)
2	–2, –1, 0, +1, +2	5 (d)
3	–3, –2, –1, 0, +1, +2, +3	7 (f)

> The number of orbitals in a given shell = n².

4. Spin Quantum Number (mₛ):

>This quantum number has no relation with the solution of Schrodinger wave equation.

> German physicists Stern and Gerlach passed a beam of neutral vapour silver atoms between the poles of a specially designed magnet. The beam was found to split into two separate beams. It was assumed that the unpaired electron present in silver atom is responsible for the split of beam. Half of the silver atoms with the unpaired electrons behave like one type of magnet and the other half behaved the opposite.

> Electron spins around its own axis along with its orbital motion. This spin creates a small magnetic field for which an electron acts like a tiny magnet. An electron can spin either clockwise or anticlockwise. Accordingly there are two spin values possible for an electron while present in an orbital.

What It Tells Us:

> The spin direction of the electron

Values:

> mₛ = +½ (spin-up or clockwise spin or aligned with the external magnetic field)

> mₛ = –½ (spin-down or anticlockwise spin or aligned against the external magnetic field)

> Each orbital (combination of n, ℓ, mₗ) can hold 2 electrons, each with opposite spin.

> The spin angular momentum of an electron is given by [s(s+1)]^1/2(h/2 π). Putting the value of s=1/2 for an electron the spin angular momentum for an electron can be calculated.

> The z component of the spin angular momentum has two possible values. They are ½ (h/2 π) and -1/2 (h/2 π).

Image Credit:

1. Emission of energy from electron 1:

By JabberWok, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=2639910

2. Emission of energy from electron 1:

By A_hidrogen_szinkepei.jpg: User:Szdoriderivative work: OrangeDog (talk • contribs) - A_hidrogen_szinkepei.jpg, CC BY 2.5, https://commons.wikimedia.org/w/index.php?curid=6273602

3. Energy level diagram as straight lines

By Rajettan - Own work, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=41466201

4. Actual obsevation of line spectrum

By OrangeDog, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=6278485